Finding Maxima and Minima using Derivatives

Where is a function at a high or low bespeak? Calculus can assistance!

A maximum is a high point and a minimum is a low bespeak:

function local minimum and maximum

In a smoothly changing function a maximum or minimum is always where the function flattens out  (except for a saddle point).

Where does it flatten out? Where the slope is cipher.

Where is the slope zero? The Derivative tells us!

Let's dive right in with an example:

quadratic graph

Case: A ball is thrown in the air. Its superlative at any time t is given by:

h = 3 + 14t − 5ttwo

What is its maximum height?

Using derivatives nosotros can discover the gradient of that function:

d dt h = 0 + 14 − 5(2t)
= fourteen − 10t

(See below this example for how we found that derivative.)

quadratic graph

Now find when theslope is naught:

xiv − 10t = 0

10t = 14

t = 14 / ten = 1.four

The slope is zero at t = 1.4 seconds

And the height at that time is:

h = 3 + 14×1.4 − five×1.42

h = iii + 19.six − nine.viii = 12.viii

And then:

The maximum peak is 12.8 m (at t = 1.four south)

A Quick Refresher on Derivatives

A derivative basically finds the slope of a function.

In the previous example we took this:

h = 3 + 14t − 5t2

and came upwards with this derivative:

d dt h = 0 + 14 − 5(2t)
= 14 − 10t

Which tells us the slope of the function at whatsoever time t

slope examples: y=3, slope=0; y=2x, slope=2

We used these Derivative Rules:

  • The gradient of a constant value (like 3) is 0
  • The slope of a line similar 2x is 2, so 14t has a slope of fourteen
  • A square role like t2 has a slope of 2t, then 5t2 has a gradient of five(2t)
  • And and so we added them up: 0 + 14 − 5(2t)

How Do We Know information technology is a Maximum (or Minimum)?

Nosotros saw it on the graph! But otherwise ... derivatives come up to the rescue again.

Take the derivative of the slope (the 2d derivative of the original function):

The Derivative of 14 − 10t is −10

This means the gradient is continually getting smaller (−10): traveling from left to right the slope starts out positive (the function rises), goes through zero (the flat point), so the slope becomes negative (the function falls):

slope positive then zero then negative
A gradient that gets smaller (and goes though 0) means a maximum.

This is called the 2d Derivative Test

On the graph higher up I showed the slope before and afterward, merely in practice we practise the examination at the point where the gradient is zip:

Second Derivative Test

When a function'south slope is zero at x, and the 2nd derivative at ten is:

  • less than 0, it is a local maximum
  • greater than 0, information technology is a local minimum
  • equal to 0, then the exam fails (at that place may be other means of finding out though)

"Second Derivative: less than 0 is a maximum, greater than 0 is a minimum"

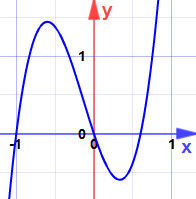
Example: Notice the maxima and minima for:

y = 5x3 + 2x2 − 3x

The derivative (gradient) is:

d dx y = 15xtwo + 4x − 3

Which is quadratic with zeros at:

  • x = −3/v
  • x = +ane/3

Could they exist maxima or minima? (Don't look at the graph yet!)

The 2nd derivative is y'' = 30x + 4

At x = −3/5:

y'' = 30(−3/five) + four = −xiv

it is less than 0, and then −three/five is a local maximum

At x = +1/iii:

y'' = thirty(+1/3) + 4 = +xiv

information technology is greater than 0, so +1/3 is a local minimum

(Now you can look at the graph.)

5x^3 2x^2 3x

Words

A loftier indicate is chosen a maximum (plural maxima ).

A depression signal is called a minimum (plural minima ).

The general word for maximum or minimum is extremum (plural extrema).

We say local maximum (or minimum) when in that location may be higher (or lower) points elsewhere simply not nearby.

One More Example

Example: Find the maxima and minima for:

y = ten3 − 6x2 + 12x − v

The derivative is:

d dx y = 3x2 − 12x + 12

Which is quadratic with only one zilch at x = ii

Is it a maximum or minimum?

The 2d derivative is y'' = 6x − 12

At x = two:

y'' = 6(two) − 12 = 0

information technology is 0, then the test fails

And here is why:

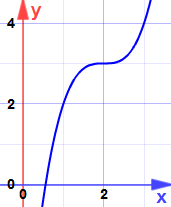
x^3 6x^2 12x 5

It is an Inflection Bespeak ("saddle signal") ... the slope does become cipher, but it is neither a maximum nor minimum.

Must Exist Differentiable

And there is an important technical point:

The function must exist differentiable (the derivative must exist at each point in its domain).

Example: How about the function f(x) = |x| (accented value) ?

|x| looks like this: Absolute Value function

At x=0 it has a very pointy change!

In fact it is not differentiable there (as shown on the differentiable page).

So nosotros can't apply the derivative method for the absolute value role.

The function must also be continuous, just any function that is differentiable is also continuous, so we are covered.